Exponential & logistic growth

Exponential & logistic growth


Modeling population growth rates
To understand the different models that are used to represent population dynamics, let's start by looking at a general equation for the population growth rate (change in number of individuals in a population over time):

In this equation, dN/dT is the growth rate of the population a given instant, N is population size, T is time, and r is the per capita rate of increase –that is, how quickly the population grows per individual already in the population.
If we assume no movement of individuals into or out of the population, r is just a function of birth and death rates. You can learn more about the meaning and derivation of the equation here:
The equation above is very general, and we can make more specific forms of it to describe two different kinds of growth models: exponential and logistic.
  • When the per capita rate of increase (r) takes the same positive value regardless of the population size, then we get exponential growth.
  • When the per capita rate of increase (r) decreases as the population increases towards a maximum limit, then we get logistic growth.
Here's a sneak preview – don't worry if you don't understand all of it yet:

Exponential growth

Bacteria grown in the lab provide an excellent example of exponential growth. In exponential growth, the population’s growth rate increases over time, in proportion to the size of the population.
Let’s take a look at how this works. Bacteria reproduce by binary fission (splitting in half), and the time between divisions is about an hour for many bacterial species. To see how this exponential growth, let's start by placing 1000 bacteria in a flask with an unlimited supply of nutrients.
  • After 1 hour: Each bacterium will divide, yielding 2000 bacteria (an increase of 1000 bacteria).
  • After 2 hours: Each of the 2000 bacteria will divide, producing 4000 (an increase of 2000 bacteria).
  • After 3 hours: Each of the 4000 bacteria will divide, producing 8000 (an increase of 4000 bacteria).
The key concept of exponential growth is that the population growth rate —the number of organisms added in each generation—increases as the population gets larger. And the results can be dramatic: after 1 day (24 cycles of division), our bacterial population would have grown from 1000 to over 16 billion! When population size, N, is plotted over time, a J-shaped growth curve is made.
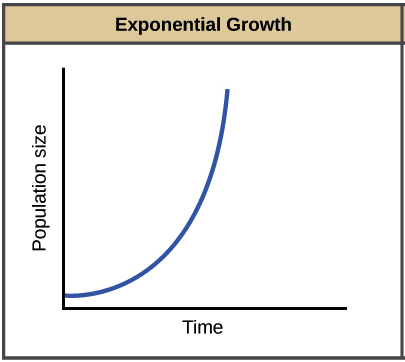
How do we model the exponential growth of a population? As we mentioned briefly above, we get exponential growth when r (the per capita rate of increase) for our population is positive and constant. While any positive, constant r can lead to exponential growth, you will often see exponential growth represented with an r of r, start subscript, m, a, x, end subscript.
r, start subscript, m, a, x, end subscript is the maximum per capita rate of increase for a particular species under ideal conditions, and it varies from species to species. For instance, bacteria can reproduce much faster than humans, and would have a higher maximum per capita rate of increase. The maximum population growth rate for a species, sometimes called its biotic potential, is expressed in the following equation:
Logistic growth
Exponential growth is not a very sustainable state of affairs, since it depends on infinite amounts of resources (which tend not to exist in the real world).
Exponential growth may happen for a while, if there are few individuals and many resources. But when the number of individuals gets large enough, resources start to get used up, slowing the growth rate. Eventually, the growth rate will plateau, or level off, making an S-shaped curve. The population size at which it levels off, which represents the maximum population size a particular environment can support, is called the carrying capacity, or K.


We can mathematically model logistic growth by modifying our equation for exponential growth, using an r (per capita growth rate) that depends on population size (N) and how close it is to carrying capacity (K). Assuming that the population has a base growth rate of r ​max when it is very small, we can write the following equation:
Let's take a minute to dissect this equation and see why it makes sense. At any given point in time during a population's growth, the expression K-N tells us how many more individuals can be added to the population before it hits carrying capacity. (K - N)/K, then, is the fraction of the carrying capacity that has not yet been “used up.” The more carrying capacity that has been used up, the more the (K - N)/K term will reduce the growth rate.
When the population is tiny, N is very small compared to K. The (K - N)/K term becomes approximately (K/K) or 1, giving us back the exponential equation. This fits with our graph above: the population grows near-exponentially at first, but levels off more and more as it approaches K

Role of intraspecific competition
The logistic model assumes that every individual within a population will have equal access to resources and, thus, an equal chance for survival. For plants, the amount of water, sunlight, nutrients, and the space to grow are the important resources, whereas in animals, important resources include food, water, shelter, nesting space, and mates.
In the real world, the variation of phenotypes among individuals within a population means that some individuals will be better adapted to their environment than others. The resulting competition between population members of the same species for resources is termed intraspecific competition (intra- = "within"; -specific = "species"). Intraspecific competition for resources may not affect populations that are well below their carrying capacity as resources are plentiful and all individuals can obtain what they need. However, as population size increases, this competition intensifies. In addition, the accumulation of waste products can reduce an environment's carrying capacity.

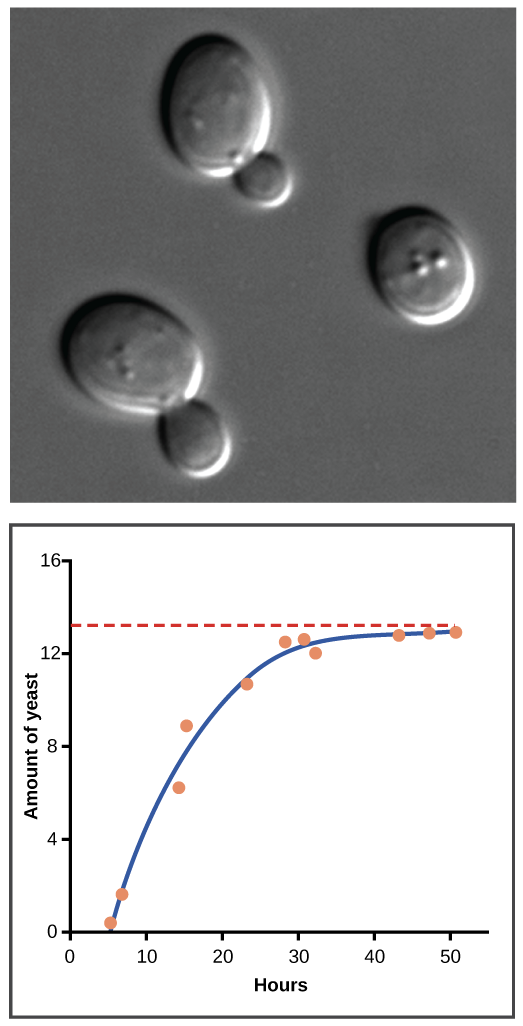
Examples of logistic growthYeast, a microscopic fungus used to make bread and alcoholic beverages, can produce a classic S-shaped curve when grown in a test tube. In the graph shown below, yeast growth levels off as the population hits the limit of the available nutrients. (If we followed the population for longer, it would likely crash, since the test tube is a closed system – meaning that fuel sources would eventually run out and wastes might reach toxic levels).
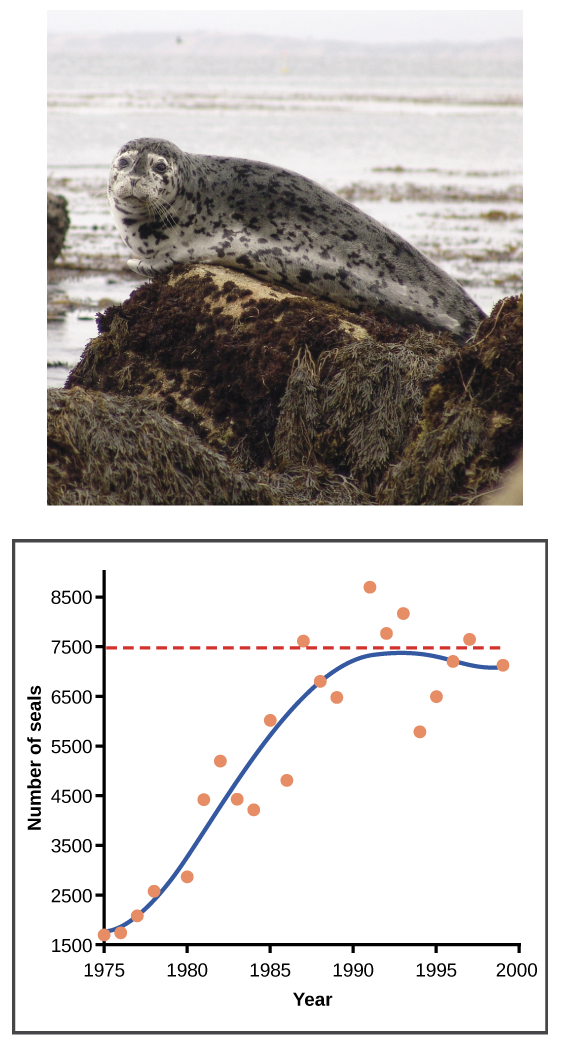
In the real world, there are variations on the “ideal” logistic curve. We can see one example in the graph below, which illustrates population growth in harbor seals in Washington State. In the early part of the 20th century, seals were actively hunted under a government program that viewed them as harmful predators, greatly reducing their numbers. Since this program was shut down, seal populations have rebounded in a roughly logistic pattern

Komentar

  1. Asmaul Khusna15 Mei 2017 pukul 07.42

    woww informasinya sangat jelas dan rapi. tapi dapatkah individu yang termasuk exponential growth menjadi logistic growth dan sebaliknya? terimakasih :)

    BalasHapus

Posting Komentar

Postingan populer dari blog ini

Tolerance range

Gambar
Tolerance Range in biology refers to the specifications of environment in which particular species can survive. These environmental factors include temperature, humidity, salinity, quality of soil and quality of air. Tolerance range differs from one species to another. Factors included in tolerance range differ too. For plants, crucial environmental conditions include sunlight and minerals in soil, whereas for animals temperature and quality of air are important. For both plants and animal, a certain amount of nutrients must be available to them to consume in order to survive. Range of tolerance also varies within a given population, from individual to individual, and across a life cycle of one individual. If living organisms find themselves within their range tolerance, they can maintain homeostasis, meaning the internal conditions necessary for carrying out their life functions. The optimum range is the mid-point on the scale of tolerance range, where most individuals in a popul
Baca selengkapnya

Limiting Factors

Gambar
• Condition is abiotic environmental factor that varies in space and time and affects the performance of organism. Example is temperature can affect the reproduction of organism because to matting and lay the egg, need a warm temperature. • Resource is all things consumed (used up) by organisms (space, nutrients, water, prey, holes for refuge, etc) and its can devided into  Interactive resources. An organism does not need certain resources independently. For example, one that gets more heat might need more water, or less nitrogen.  Non-interactive resources. Independent resources that an organism needs. For example, a human being needs both iron and calcium, though ingesting one will not affect the need for the other. Liebig’s law of the minimum: Growth of a plant is dependent on the amount of foodstuff which is presented to it in minimum quantity. This law of the minimum was first expressed by Justus Liebig in 1840. This law of the minimum is less applicable under ‘transien
Baca selengkapnya

Ectoterm dan Endoterm

Gambar
Ectothermic animals Ectothermic animals are animals that are very dependent on the temperature in the external environment to increase its body temperature due to the heat generated from the whole system of metabolism only slightly. Ektoterm animals, a group of animals whose body heat depending on the heat from the outside of the body, namely the environment. Power regulator for temperature is very limited and its body temperature varies with the temperature of the environment. This causes poikilotherm animals have a low tolerance range, in the sense that this animal narrow niche subject. When the ambient temperature is high, beyond the limits tolerance, ektoterm animals will die while when the ambient temperature is lower than the optimum temperature, activity was low and the animal becomes very slow, making it easy for predators to catch. Power set in animals ektoterm and not of physiological adaptation but rather in the form of behavioral adaptation. For example, moves to the sha
Baca selengkapnya